「python」カテゴリーアーカイブ

python

関数set.issupersetの使い方の例

関数の機能：この集合が別の集合を含んでいるか判定

例1 : Trueが返却される場合

>>> set1 = {'A', 'B', 'C'}
>>> set2 = {'A', 'B'}
>>> set1.issuperset(set2)
True
この例では、set2の全ての要素がset1に有り、set2をset1が含んでいる状態なのでTrueが返却されています。

例2 : Falseが返却される場合

>>> set1 = {'A', 'B', 'C'}
>>> set2 = {'A', 'D'}
>>> set1.issuperset(set2)
False
この例では、set2のうち'D'の要素がset1には無く、set1はset2を含んでいない状態なのでFalseが返却されています。

関連項目

関数set.isdisjointの使い方の例
関数set.issubsetの使い方の例
python

関数set.issubsetの使い方の例

関数の機能：別の集合にこの集合が含まれているか判定

例1 : Trueが返却される場合

>>> set1 = {'A', 'B'}
>>> set2 = {'A', 'B', 'C'}
>>> set1.issubset(set2)
True
この例では、set1の全ての要素がset2に有り、set1がset2に含まれている状態なのでTrueが返却されています。

例2 : Falseが返却される場合

>>> set1 = {'A', 'B'}
>>> set2 = {'A', 'C', 'D'}
>>> set1.issubset(set2)
False
この例では、set1のうち'B'の要素がset2には無く、set1はset2に含まれていない状態なのでFalseが返却されています。

関連項目

関数set.isdisjointの使い方の例
関数set.issupersetの使い方の例
python

関数set.isdisjointの使い方の例

関数の機能：別の集合と共通の要素が無いことを判定

例1 : Trueが返却される場合

>>> set1 = {'A', 'B'}
>>> set2 = {'X', 'Y'}
>>> set1.isdisjoint(set2)
True
set1とset2の両方に存在する要素が1つも無いのでTrueが返却されています。

例2 : Falseが返却される場合

>>> set1 = {'A', 'B'}
>>> set2 = {'B', 'C'}
>>> set1.isdisjoint(set2)
False
set1とset2の両方に'B'が存在するのでFalseが返却されています。

関連項目

関数set.issubsetの使い方の例
関数set.issupersetの使い方の例
python

関数set.removeの使い方の例

関数の機能：集合から要素を削除
        （指定した要素が無ければエラーが発生）

例1 : 要素が削除される場合

>>> set1 = {'A', 'B', 'C'}
>>> set1.remove('C')
>>> set1
{'A', 'B'}
このように、引数で指定した要素が集合にあれば削除されます。

例2 : 指定した要素が集合に無い場合

>>> set1 = {'A', 'B', 'C'}
>>> set1.remove('Z')
Traceback (most recent call last):
...
KeyError: 'Z'
引数で指定した要素が集合に無ければエラーが発生します。

関連項目

関数set.addの使い方の例
関数set.clearの使い方の例
関数set.discardの使い方の例
関数set.popの使い方の例
python

関数set.popの使い方の例

関数の機能：集合から要素をどれか1つ取り出す（返却・削除する）

3要素の集合から要素を1 つずつ取り出す

>>> set1 = {'A', 'B', 'C'}
>>> set1.pop()
'A'
>>> set1
{'C', 'B'}
>>> set1.pop()
'C'
>>> set1
{'B'}
>>> set1.pop()
'B'
>>> set1
set()
　3要素の集合から要素を1つずつ取り出した例です。1回関数を呼び出すごとに要素が1つずつ減り、最後は空集合となっています。
　なお、集合には要素の順番が決められていませんので、リストの関数popのように最後の要素が対象となるということはなく、特にルールは無くどれか1つの要素が選択されて返却・削除されます。。

空の集合に関数popを使用するとエラー

>>> set1.pop()
Traceback (most recent call last):
...
KeyError: 'pop from an empty set'
　このように、空の集合に関数popを使用するとエラーが発生します。

関連項目

関数set.addの使い方の例
関数set.clearの使い方の例
関数set.discardの使い方の例
関数set.removeの使い方の例
python

関数set.discardの使い方の例

関数の機能：集合から要素を削除
        （指定した要素が無ければ何もしない）

例1 : 要素が削除される場合

>>> set1 = {'A', 'B', 'C'}
>>> set1.discard('B')
>>> set1
{'C', 'A'}
このように、引数で指定した要素が集合にあれば削除されます。

例2 : 要素が削除されない場合

>>> set1 = {'A', 'B', 'C'}
>>> set1.discard('Z')
>>> set1
{'B', 'C', 'A'}
このように、引数で指定した要素が集合に無ければ集合に変化はありません。

関連項目

関数set.addの使い方の例
関数set.clearの使い方の例
関数set.popの使い方の例
関数set.removeの使い方の例
python

関数set.symmetric_difference(_update)の使い方の例

関数の機能:
  集合の対称差(setAとsetBの1つだけにある要素の集合）を求める

    setA.symmetric_difference(setB)
    setA.symmetric_difference_update(setB)
  
  symmetric_difference : 
    集合の対称差を返却
    (setAは変更されない)
  symmetric_difference_update : 
    関数を呼び出した集合が集合の対称差に変更される
    (setAが変更される, 返却値はNone)

例1 : 2つの集合の対称差

>>> set1 = {'A', 'B', 'C'}
>>> set2 = {'B', 'C', 'D'}
>>> set1.symmetric_difference(set2)
{'D', 'A'}
この例では、set1とset2の1つだけにある要素の集合が関数から返却されています。
この例のイメージを下図に示します。集合の対称差は図中の青い部分で、この部分の集合が関数から返却されます。
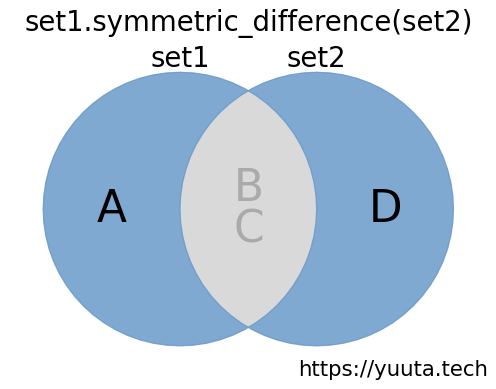
集合の対称差の説明
なお、関数の呼び出し後にset1の内容を確認すると更新されていないことがわかります。
>>> set1
{'C', 'B', 'A'}
この関数を使う代わりに ^ 演算子を使用して下記のように記述することもできます。
>>> set1 ^ set2
{'D', 'A'}
difference_updateを使用した場合は下記のようになります。
>>> set1.symmetric_difference_update(set2)
>>> set1
{'A', 'D'}

例2 : 3つの集合の対称差

>>> set1 = {'A', 'B', 'C'}
>>> set2 = {'B', 'D'}
>>> set3 = {'C', 'E'}
>>> set1.symmetric_difference(set2, set3)
Traceback (most recent call last):
...
TypeError: set.symmetric_difference() takes exactly one argument (2 given)
関数symmetric_differenceは、引数に複数の集合を指定することができない仕様となっていますので、エラーが発生します。
^ の演算子を使用して下記のように記述することはできます。
>>> set1 ^ set2 ^ set3
{'D', 'E', 'A'}

関連項目

関数set.difference(_update)の使い方の例
関数set.intersection(_update)の使い方の例
関数set.union, set.updateの使い方の例
python

関数set.union, set.updateの使い方の例

関数の機能:
  集合の和(setAとsetBのいずれかに含まれる要素の集合）を求める

    setA.union(setB)
    setA.update(setB)
  
  union : 
    集合の和を返却
    (setAは変更されない)
  update : 
    関数を呼び出した集合が集合の和に変更される
    (setAが変更される, 返却値はNone)

例1 : 2つの集合の和

>>> set1 = {'A', 'B', 'C'}
>>> set2 = {'B', 'C', 'D'}
>>> set1.union(set2)
{'A', 'D', 'C', 'B'}
この例では、set1とset2のいずれかに含まれる要素を持つ集合が関数から返却されています。
この例のイメージを下図に示します。集合の和は図中の青い部分で、この部分の集合が関数から返却されます。
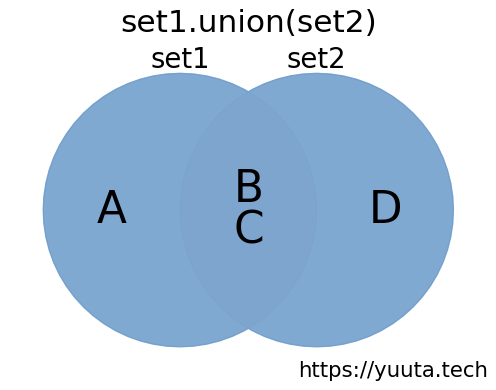
集合の和の説明
なお、関数の呼び出し後にset1の内容を確認すると更新されていないことがわかります。
>>> set1
{'C', 'B', 'A'}
| 演算子を使用して下記のように記述することもできます。
>>> set1 | set2
{'A', 'D', 'C', 'B'}
updateを使用した場合は下記のようになります。
>>> set1.update(set2)
>>> set1
{'A', 'D', 'C', 'B'}

例2 : 3つの集合の和

>>> set1 = {'A', 'B', 'C'}
>>> set2 = {'B', 'C', 'D'}
>>> set3 = {'C', 'D', 'E'}
>>> set1.union(set2, set3)
{'E', 'A', 'D', 'C', 'B'}
この例では、set1とset2とset3のいずれかに含まれる要素を持つ集合が関数から返却されています。
| の演算子を使用して下記のように記述することもできます。
>>> set1 | set2 | set3
{'E', 'A', 'D', 'C', 'B'}

関連項目

関数set.difference(_update)の使い方の例
関数set.intersection(_update)の使い方の例
関数set.symmetric_difference(_update)の使い方の例
python

関数set.intersection(_update)の使い方の例

関数の機能:
  集合の積(setAとsetBの共通部分の集合）を求める

    setA.intersection(setB)
    setA.intersection_update(setB)
  
  intersection : 
    集合の積を返却
    (setAは変更されない)
  intersection_update : 
    関数を呼び出した集合が集合の積に変更される
    (setAが変更される, 返却値はNone)

例1 : 2つの集合の積

>>> set1 = {'A', 'B', 'C'}
>>> set2 = {'B', 'C', 'D'}
>>> set1.intersection(set2)
{'B', 'C'}
この例では、set1とset2の両方に含まれる要素を持つ集合が関数から返却されています。
この例のイメージを下図に示します。集合の積は図中の青い部分で、この部分の集合が関数から返却されます。
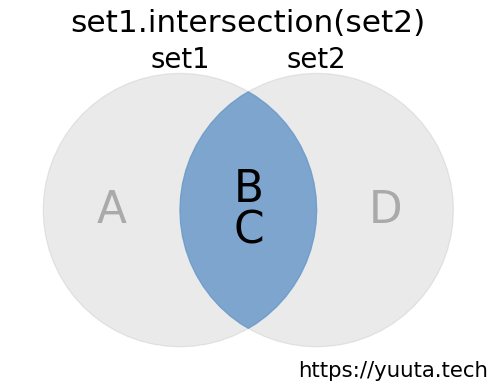
集合の積の説明
なお、関数の呼び出し後にset1の内容を確認すると更新されていないことがわかります。
>>> set1
{'A', 'B', 'C'}
& 演算子を使用して下記のように記述することもできます。
>>> set1 & set2
{'B', 'C'}
intersection_updateを使用した場合は下記のようになります。
>>> set1.intersection_update(set2)
>>> set1
{'B', 'C'}

例2 : 3つの集合の積

>>> set1 = {'A', 'B', 'C'}
>>> set2 = {'B', 'C', 'D'}
>>> set3 = {'C', 'D', 'E'}
>>> set1.intersection(set2, set3)
{'C'}
この例では、set1とset2とset3の全てに含まれる要素を持つ集合が関数から返却されています。
& の演算子を使用して下記のように記述することもできます。
>>> set1 & set2 & set3
{'C'}

関連項目

関数set.difference(_update)の使い方の例
関数set.symmetric_difference(_update)の使い方の例
関数set.union, set.updateの使い方の例